Retarded Green’s Function Calculation

This tutorial demonstrates how to compute the retarded Green’s function for a strongly correlated lattice model using the isqham library.

Objectives

  • Understand the structure of the lattice Hamiltonian.

  • Learn how to compute the time evolution of Green’s function.

  • Visualize the results with NumPy and Matplotlib.

[1]:

import numpy as np
from c_fusion import CFusion

from isqham.greenfunction.frequencyGreenf import GreenFuncZ
from isqham.greenfunction.LatticeGreen import LatticeGreenFunction
from isqham.greenfunction.retardedGreenfunction import RetardedGreenFunction
from isqham.lattice.fermionLattice import getLatticeHam, getSupH

[2]:

U = 3
N = 60

tMax = 30
tN = 100
eta = 0.2

supH = getSupH(U=U)
clusterH = getLatticeHam(U=U)


def optimized_phi(t, U, V):
    alpha = (U - V) / 4
    beta = (t**2 + alpha**2) ** 0.5
    sin = (alpha - beta) / (((alpha - beta) ** 2 + t**2) ** 0.5)
    phi = -np.arcsin(sin) * 2
    return phi


phi0 = optimized_phi(t=-1, U=U, V=0)


def get_gs():
    gs = CFusion(4)
    gs.RY(0, phi0)
    gs.CNOT(0, 1).CNOT(1, 2).CNOT(2, 3)
    gs.Y2M(0)
    gs.X(1).X(3)
    gs.CNOT(0, 1).CNOT(1, 2).CNOT(2, 3)
    return gs


gs = get_gs()

### set Green's function generator
gt = RetardedGreenFunction(
    H=clusterH, N=N, circuit_cls=CFusion, ground_state=gs, shots=1024
)
gz = GreenFuncZ(tMax=tMax, tN=tN, rGObj=gt)
latG = LatticeGreenFunction(GZ=gz, supH=supH)


OmegaMax = 6.0
Gamma = np.array([0.0, 0.0, 0.0])
X = np.array([0, np.pi, 0.0])
M = np.array([np.pi, np.pi, 0.0])
kPoints = [Gamma, X, M, Gamma]
Omega = np.arange(-OmegaMax, OmegaMax, 0.1)

rho = latG.getDensityOfState(
    kPoints=kPoints, OmegaPoints=Omega, eta=eta, kMesh=40, index=[0]
)

[3]:

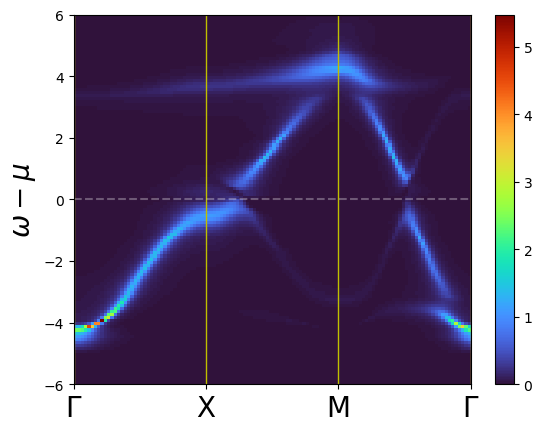
import matplotlib.pyplot as plt

fig = plt.figure()
ax = plt.axes()

Xlablist = [r"$\Gamma$", "X", "M", r"$\Gamma$"]
extent = (0, len(Xlablist) - 1, -6, 6)

imsh = ax.imshow(
    rho, extent=extent, cmap="turbo", aspect="auto", vmin=0, vmax=rho.max()
)

bar = plt.colorbar(imsh)

ax.set_xticks(range(len(Xlablist)))
ax.set_xticklabels(Xlablist, size=20)
ax.set_ylabel(r"$\omega-\mu$", size=20)
ax.xaxis.grid(True, which="major", color="y", linestyle="-", linewidth=1)
plt.plot([0, 3], [0, 0], "--", color="w", alpha=0.3)

[3]:

[<matplotlib.lines.Line2D at 0x7f2b6d6c15e0>]
../../_images/tutorials_green_function_retarded_gf_calc_3_1.png

Appendix: Notes and References