Quantum-Classical Hybrid Neural Network¶
Basic Parameter Setup¶
We fix the random seed to ensure reproducibility.
[13]:
import random
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
from torch.utils.data import DataLoader
from isqtools import IsqCircuit
from isqtools.backend import TorchBackend
from isqtools.neural_networks import TorchLayer
def setup_seed(seed):
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
np.random.seed(seed)
random.seed(seed)
setup_seed(222)
Set the hyperparameters.
[14]:
epochs = 1
train_samples = 200
batch_size_train = 10
test_samples = 100
batch_size_test = 10
device = "cpu"
Data Loading¶
Download the MNIST dataset. For simplicity, we extract only the samples labeled as digits 0 and 1.
[15]:
train_data = torchvision.datasets.MNIST(
"./data/",
train=True,
download=True,
transform=torchvision.transforms.Compose(
[
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,),
(0.3081,),
),
]
),
)
test_data = torchvision.datasets.MNIST(
"./data/",
train=False,
download=True,
transform=torchvision.transforms.Compose(
[
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,),
(0.3081,),
),
]
),
)
idx = np.append(
np.where(train_data.targets == 0)[0][:train_samples],
np.where(train_data.targets == 1)[0][:train_samples],
)
train_data.data = train_data.data[idx]
train_data.targets = train_data.targets[idx]
train_dataloader = DataLoader(
train_data,
batch_size=batch_size_train,
shuffle=True,
)
# label X_train, y_train
idx = np.append(
np.where(test_data.targets == 0)[0][:test_samples],
np.where(test_data.targets == 1)[0][:test_samples],
)
test_data.data = test_data.data[idx]
test_data.targets = test_data.targets[idx]
test_dataloader = DataLoader(test_data, batch_size=batch_size_test, shuffle=True)
# label X_test, y_test
Inspect the Dataset¶
We visualize a few samples from the filtered MNIST dataset (digits 0 and 1) to verify the data loading process and confirm that the input images and corresponding labels are correct.
[16]:
test_plot_data, test_plot_targets = next(iter(test_dataloader))
_, axes = plt.subplots(1, 8, figsize=(10, 3))
for i in range(8):
axes[i].imshow(test_plot_data[i][0], cmap="gray", interpolation="none")
axes[i].set_title(f"Number: {test_plot_targets[i]}")
axes[i].set_xticks([])
axes[i].set_yticks([])

Create the Quantum Circuit for the Hybrid Model¶
The quantum circuit is defined in the hybrid.isq file. We use tempfileto simulate here
[17]:
FILE_CONTENT = """\
import std;
param inputs[], weights[];
qbit q[2];
procedure single_h(qbit q[]) {
for i in 0:q.length {
H(q[i]);
}
}
procedure adjacent_cz(qbit q[]) {
for i in 0:q.length-1 {
CZ(q[i], q[i+1]);
}
}
procedure encode_inputs(qbit q[], int start_idx) {
for i in 0:q.length {
Rz(inputs[i+start_idx], q[i]);
}
}
procedure encode_weights(qbit q[], int start_idx) {
for i in 0:q.length {
Rx(weights[i+start_idx], q[i]);
}
for i in 0:q.length {
Ry(weights[i+start_idx+q.length], q[i]);
}
for i in 0:q.length {
Rz(weights[i+start_idx+q.length*2], q[i]);
}
}
procedure main() {
single_h(q);
encode_inputs(q, 0);
adjacent_cz(q);
encode_weights(q, 0);
adjacent_cz(q);
encode_weights(q, 6);
adjacent_cz(q);
M(q[0]);
M(q[1]);
}"""
Create the quantum machine learning circuit using Python.
[18]:
import tempfile
from pathlib import Path
from isqtools.draw import Drawer
backend = TorchBackend()
with tempfile.TemporaryDirectory() as temp_dir:
temp_dir_path = Path(temp_dir)
temp_file_path = temp_dir_path / "hybrid.isq"
with open(temp_file_path, "w") as temp_file:
temp_file.write(FILE_CONTENT)
qc = IsqCircuit(
file=temp_file_path,
backend=backend,
sample=False,
)
def circuit(inputs, weights):
param = {
"inputs": inputs,
"weights": weights,
}
result = qc.measure(**param)
return torch.cat((result[0].view(-1), result[2].view(-1)))
qnn = TorchLayer(
circuit=circuit,
num_weights=12,
is_vmap=True,
)
dr = Drawer()
dr.plot(qc.qcis)
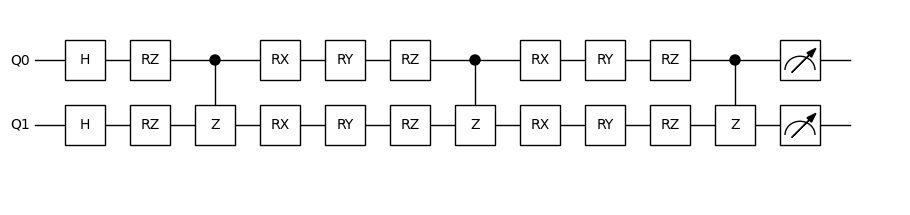
Build the Classical-Quantum Hybrid Network¶
Since qnn inherits from torch.nn.Module, it can be easily integrated into a classical neural network to form a classical-quantum hybrid model.
Here, we use a convolutional neural network (CNN) followed by fully connected layers to process image data. The qnn is inserted into the fully connected part of the network, forming the hybrid architecture.
In this setup:
The
inputstoqnnhave dimension 2.The
qnnreturns a measurement output of dimension 2.
Thus, qnn is placed between two linear layers that match this shape.
Important: Always ensure the input and output dimensions of qnn are compatible with the surrounding classical layers. Otherwise, the hybrid network cannot be constructed properly.
[19]:
class HybridNet(nn.Module):
def __init__(self, qnn):
super().__init__()
self.conv = nn.Sequential(
nn.Conv2d(1, 10, kernel_size=5),
nn.MaxPool2d(2),
nn.ReLU(),
nn.Conv2d(10, 20, kernel_size=5),
nn.Dropout2d(),
nn.MaxPool2d(2),
nn.ReLU(),
nn.Flatten(),
)
self.fc = nn.Sequential(
nn.Linear(320, 50),
nn.ReLU(),
nn.Linear(50, 2),
qnn,
nn.Linear(2, 2),
)
def forward(self, x):
x = self.conv(x)
x = self.fc(x)
return x
[20]:
hybrid_net = HybridNet(qnn)
loss_fn = nn.CrossEntropyLoss()
optimizer = optim.Adam(hybrid_net.parameters(), lr=0.001)
[21]:
def train(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset)
model.train()
for batch, (X, y) in enumerate(dataloader):
X, y = X.to(device), y.to(device)
# Compute prediction error
pred = model(X)
loss = loss_fn(pred, y)
# Backpropagation
loss.backward()
optimizer.step()
optimizer.zero_grad()
if batch % 10 == 0:
loss, current = loss.item(), (batch + 1) * len(X)
print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
def test(dataloader, model, loss_fn):
size = len(dataloader.dataset)
num_batches = len(dataloader)
model.eval()
test_loss, correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
X, y = X.to(device), y.to(device)
pred = model(X)
test_loss += loss_fn(pred, y).item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
test_loss /= num_batches
correct /= size
print(
f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n"
)
Train the Neural Network¶
Train the classical-quantum hybrid neural network for 5 epochs. During training, use standard PyTorch procedures — including forward pass, loss computation, backpropagation, and parameter updates — to optimize both classical and quantum components.
[22]:
epochs = 5
for t in range(epochs):
print(f"Epoch {t+1}\n-------------------------------")
train(train_dataloader, hybrid_net, loss_fn, optimizer)
test(test_dataloader, hybrid_net, loss_fn)
print("Done!")
Epoch 1
-------------------------------
loss: 0.822773 [ 10/ 400]
loss: 0.584339 [ 110/ 400]
loss: 0.547312 [ 210/ 400]
loss: 0.492907 [ 310/ 400]
Test Error:
Accuracy: 99.5%, Avg loss: 0.493613
Epoch 2
-------------------------------
loss: 0.521913 [ 10/ 400]
loss: 0.541909 [ 110/ 400]
loss: 0.444593 [ 210/ 400]
loss: 0.484125 [ 310/ 400]
Test Error:
Accuracy: 100.0%, Avg loss: 0.455073
Epoch 3
-------------------------------
loss: 0.465106 [ 10/ 400]
loss: 0.478267 [ 110/ 400]
loss: 0.471614 [ 210/ 400]
loss: 0.465876 [ 310/ 400]
Test Error:
Accuracy: 100.0%, Avg loss: 0.427130
Epoch 4
-------------------------------
loss: 0.424858 [ 10/ 400]
loss: 0.420086 [ 110/ 400]
loss: 0.431515 [ 210/ 400]
loss: 0.420472 [ 310/ 400]
Test Error:
Accuracy: 100.0%, Avg loss: 0.396076
Epoch 5
-------------------------------
loss: 0.414942 [ 10/ 400]
loss: 0.384991 [ 110/ 400]
loss: 0.457078 [ 210/ 400]
loss: 0.377611 [ 310/ 400]
Test Error:
Accuracy: 100.0%, Avg loss: 0.364367
Done!
Model Validation¶
Evaluate the model’s prediction accuracy on the test dataset by comparing its predicted labels with the true labels. This provides a direct measure of the classification performance of the hybrid neural network.
[23]:
count = 0
_, axes = plt.subplots(1, 8, figsize=(10, 3))
hybrid_net.eval()
with torch.no_grad():
for batch_idx, (data, target) in enumerate(test_dataloader):
if count == 8:
break
output = hybrid_net(data[0:1])
pred = output.argmax(dim=1, keepdim=True)
axes[count].imshow(data[0].numpy().squeeze(), cmap="gray", interpolation="none")
axes[count].set_xticks([])
axes[count].set_yticks([])
axes[count].set_title(f"Predicted {pred.item()}")
count += 1

Environment Information¶
The following versions of software and libraries are used in this tutorial:
[24]:
import platform
import subprocess
from importlib.metadata import version
print(f"Python version used in this tutorial: {platform.python_version()}")
print(f"Execution environment: {platform.system()} {platform.release()}\n")
isqc_version = subprocess.check_output(
["isqc", "-V"], stderr=subprocess.STDOUT, text=True
).strip()
print(f"isqc version: {isqc_version}")
isqtools_version = version("isqtools")
print(f"isqtools version: {isqtools_version}")
numpy_version = version("numpy")
print(f"NumPy version: {numpy_version}")
torch_version = version("torch")
print(f"Torch version: {torch_version}")
torchvision_version = version("torchvision")
print(f"torchvision version: {torchvision_version}")
Python version used in this tutorial: 3.13.5
Execution environment: Linux 6.12.45
isqc version: isQ Compiler 0.2.5
isqtools version: 1.4.1
NumPy version: 2.3.1
Torch version: 2.7.1
torchvision version: 0.22.1